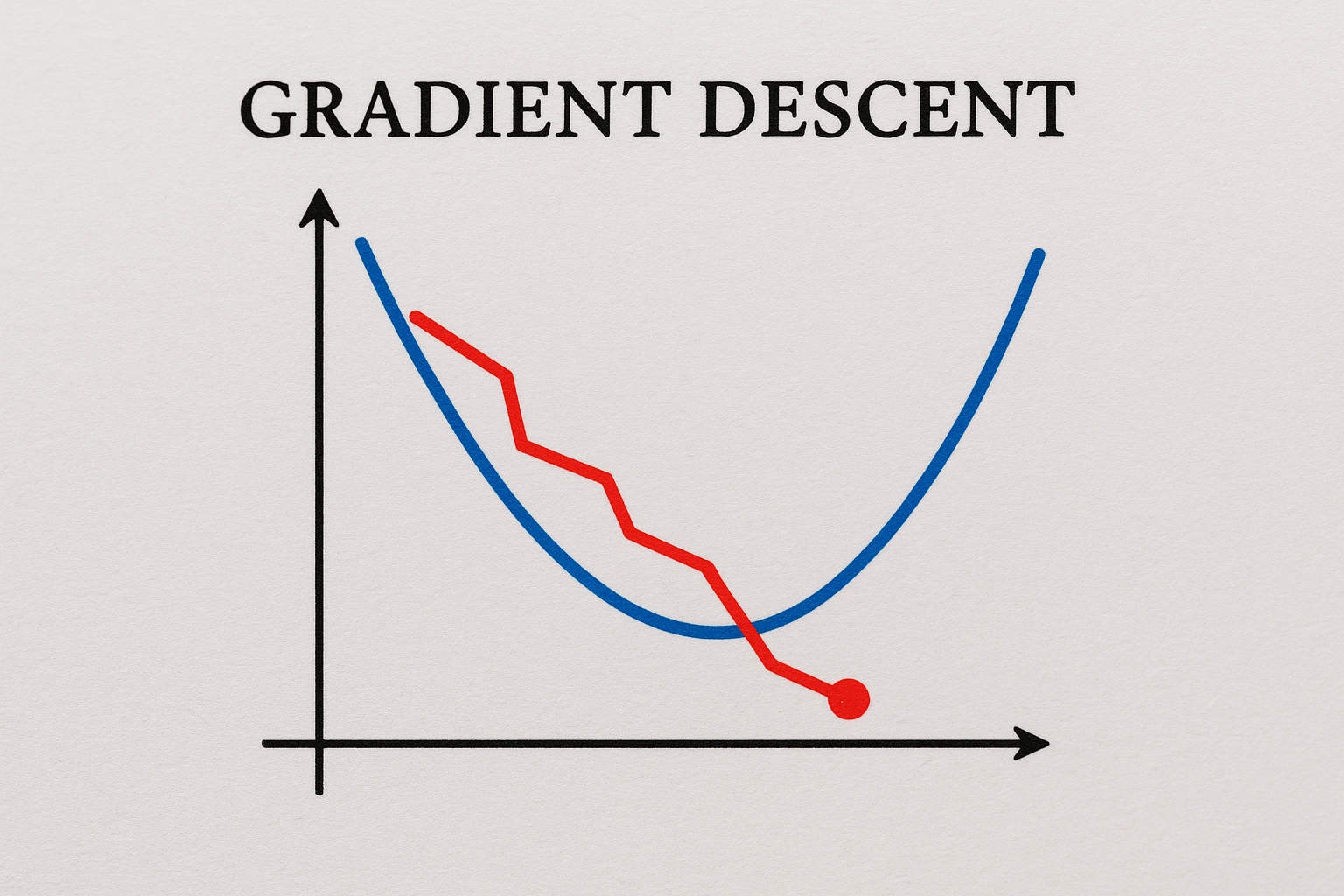
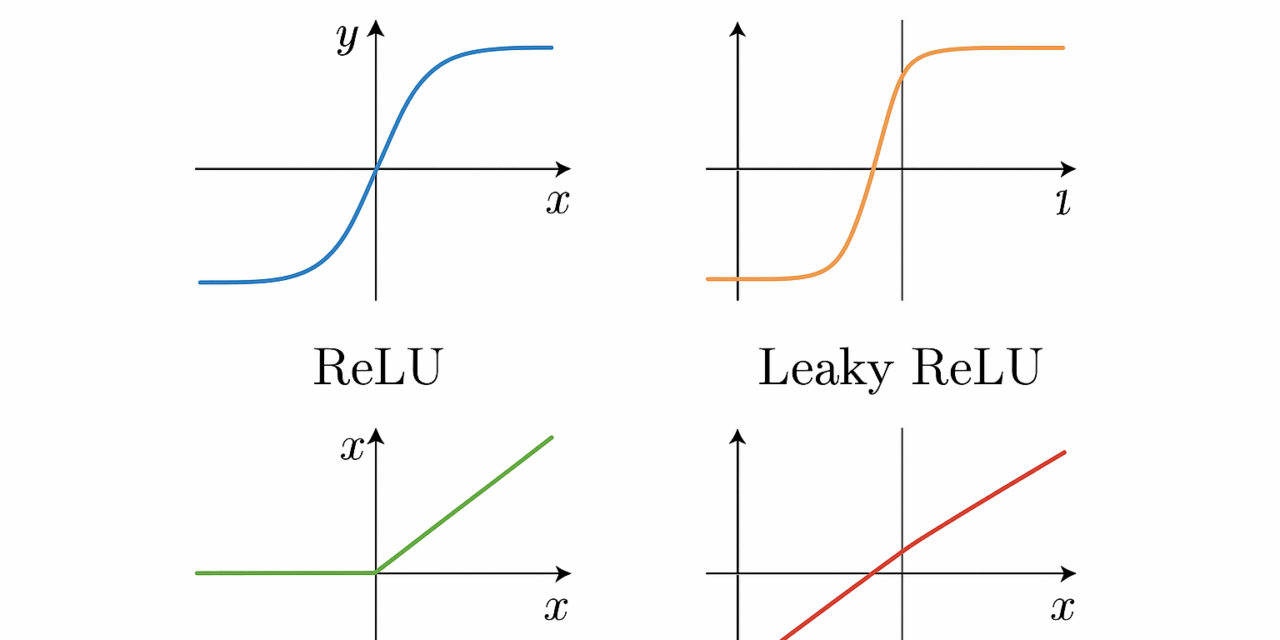最適解を見つける勾配降下法
活性化関数は、ニューラルネットワークにおけるニューロンの働きを支える重要な要素であり、入力信号を次の層に効果的に伝える役割を持っています。この関数は、シンプルな数学的処理を通じて、複雑なデータパターンを学習するための基礎を形成します。特に、非線形性を導入することで、モデルは多様なデータセットに適応でき、より豊かな表現力を獲得します。活性化関数の選択は、ネットワーク全体のパフォーマンスに直接影響を与えるため、適切な関数を用いることが成功の鍵となります。
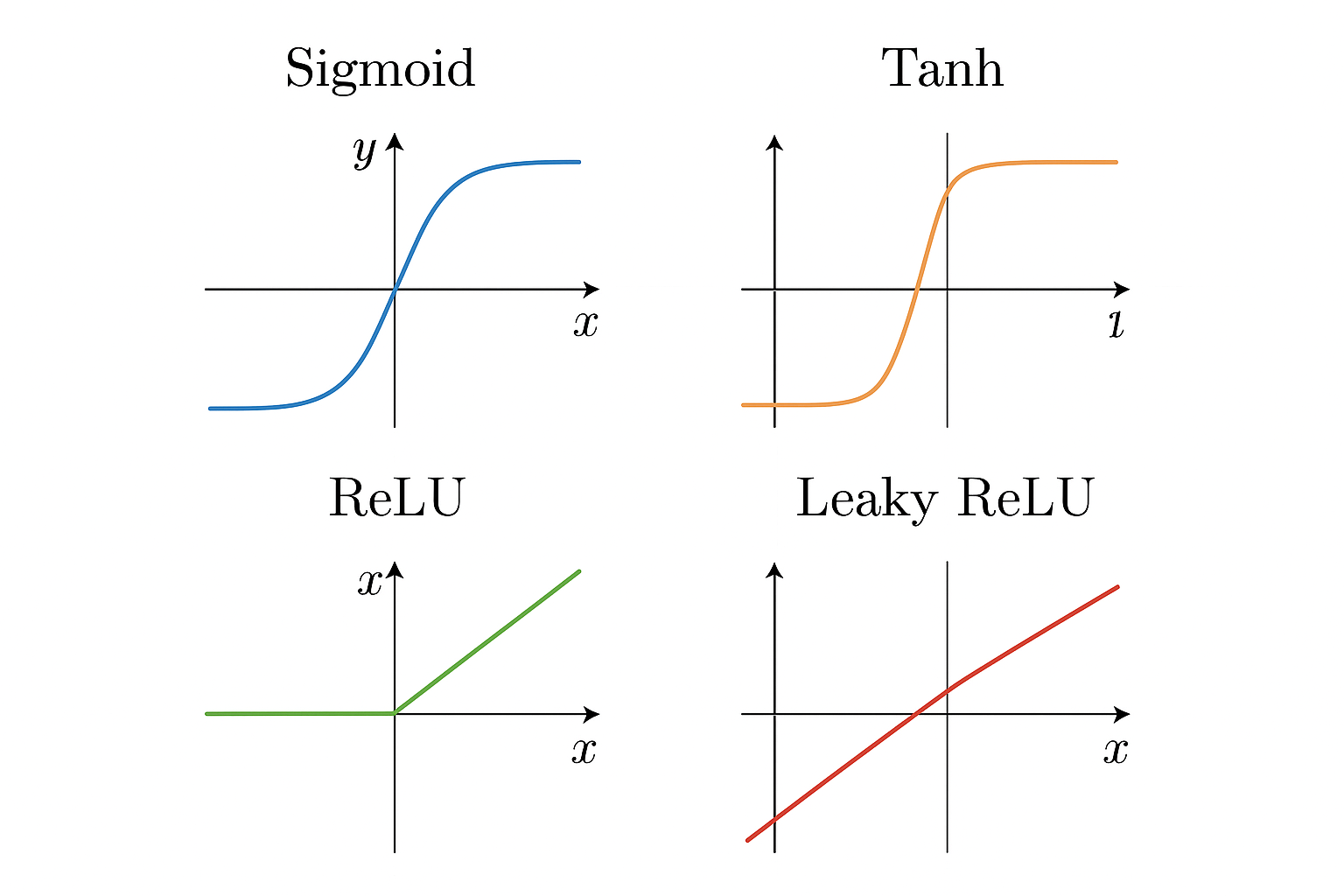
シグモイド関数
シグモイド関数は、入力信号を滑らかに変換し、ニューラルネットワークにおける出力を0から1の範囲に収束させることで、確率的な解釈を可能にします。この特性によって、モデルは複雑なデータパターンの中で重要な境界を学習でき、異なるクラス間の明確な区別を実現します。また、勾配消失問題への対策としても知られ、活性化関数の中でも特に歴史的かつ基本的な役割を果たしています。シグモイド関数の出力値は0と1の間にあるため、分類問題において特定のカテゴリーに属する確率を表現するのに便利です。
Tanh関数
Tanh関数はシグモイド関数と同様に活性化関数として広く用いられていますが、特にその出力が-1から1の範囲に収束する特性が特徴的です。この特性により、Tanh関数はデータの中心化を促進し、より迅速な収束を実現するため、勾配降下法においても非常に効果的です。ニューラルネットワークにおける非線形性の重要な要素として、Tanh関数は反復的な学習過程においてより豊かな表現能力を提供し、複雑な問題の解決に寄与します。特に多様なデータセットにおいて、Tanh関数はシグモイド関数の限界を克服し、より有効な情報伝達を可能にします。
ReLU関数
ReLU関数はそのシンプルさと効率性から、現代のニューラルネットワークにおいて非常に人気のある活性化関数の一つです。この関数は、正の入力信号をそのまま出力し、負の入力信号に対してはゼロを返す特性を持っています。その結果、ReLU関数は非線形性を効果的に導入しつつ、計算の簡素化を図ることができ、特に大規模なデータセットを扱う際にモデルの訓練速度を著しく向上させることができます。また、勾配消失問題を軽減することができるため、深層学習においてより深いネットワークを構築する際の選択肢として欠かせない存在となっています。多様な応用シナリオにおいて、その力強さを発揮し、精度の高い予測を実現するための重要な要素となっています。